Triangle Inequality

The triangle inequality may refer to one of many different theorems, all of which are similar to, derived from or generalisations of the following observation about triangles.

Given a triangle with side lengths \(a\), \(b\), and \(c\), for any choice of the labelling of the sides, \(a + b \geq c\). Note that the potential equality is only for the degenerate case, where the vertices are collinear.

In a Normed Vector Space

In a normed vector space, the triangle inequality is an explicit requirement for a vector space norm, and is stated as:

Intuition in \(\mathbb{R}^{2}\)

In \(\mathbb{R}^{2}\), the triangle inequality for the norm induced by the dot product has a clear geometric intuition that aligns with the case of a triangle described at the top of this note.

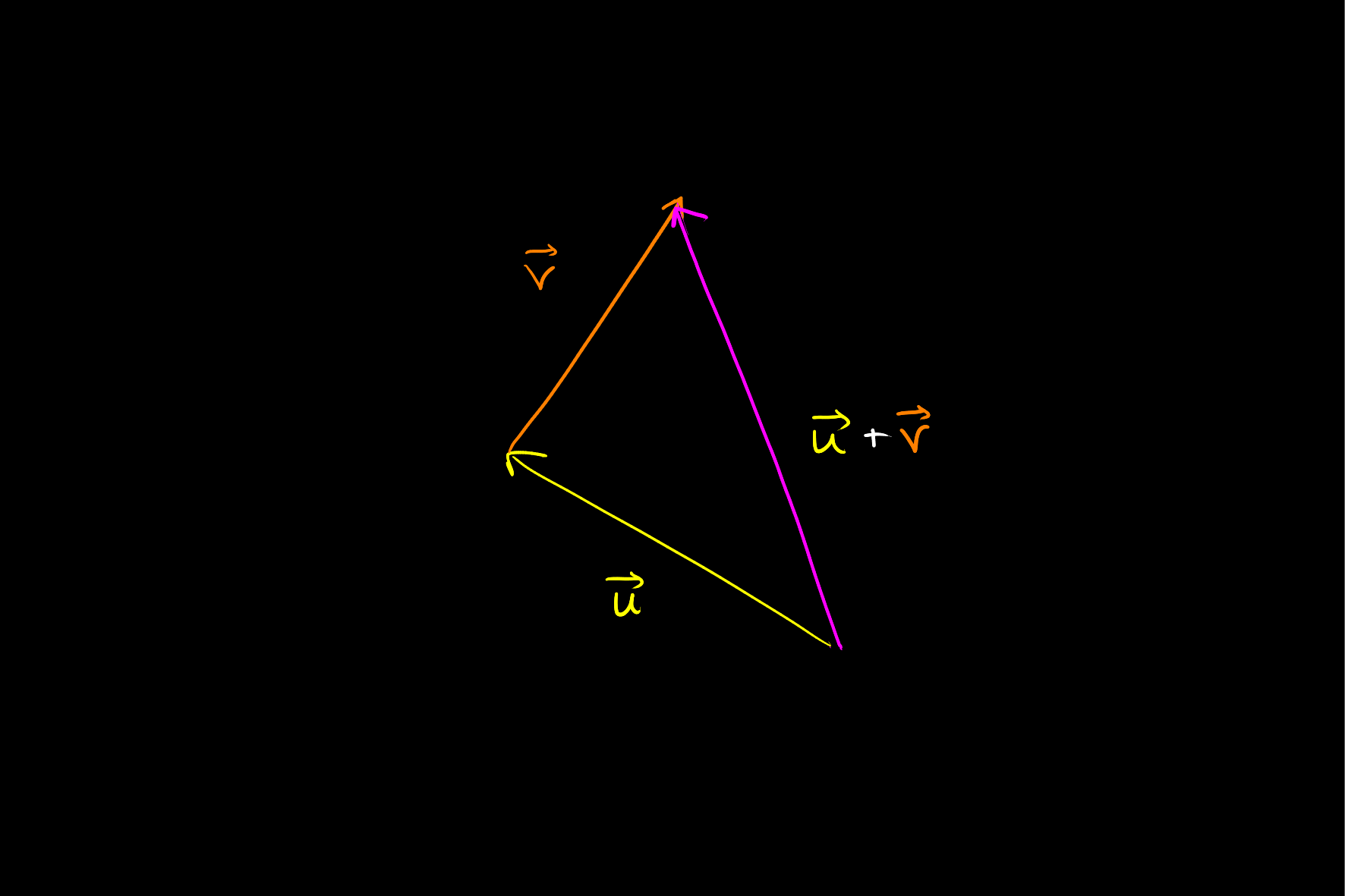
In the Context of Complex Numbers

In the context of complex numbers, the triangle inequality generally refers to:

for \(z, w \in \mathbb{C}\).

The geometric intuition in the complex plane is basically identical to that of the triangle inequality for norms in \(\mathbb{R}^{2}\).

In a Metric Space

Within a metric space, the triangle inequality, which is one of the requirements for a metric, is that:

Similarly to the case of the norm, in \(\mathbb{R}^{2}\) this geometrically represents how the length of one side of a triangle is less than or equal to the sum of the other two.